|
|
23.11.2005 Druckübertragungsringe aus Holz oder Holzwerkstoffen finden beim Vortrieb von Rohren mit druckkraftschlüssiger Steckverbindung durch Einpressen oder Einschieben am häufigsten Anwendung bedingt durch ihre sehr geringe Querdehnung. Nach ATV-A 125 [ATVA125b] kommen dafür Nadelholz (Fichte, Tanne) als astfreies Vollholz, Sperrholz oder Spanplatte (Flachpressplatte) in Frage. Im Falle des Einsatzes von Sperrholz oder Spanplatte sind ausschließlich wasserfest … |
|||
|
|
23.11.2005 Eine Möglichkeit, den klassischen Druckübertragungsring aus Holz oder Holzwerkstoff zu ersetzen, bietet der Einsatz von Kunststoffen (z.B. Polyethylen, Polyurethan, Polyamid). Der Vorteil der Kunststoffe liegt in ihrem elastischen Verhalten mit einem gegenüber Holz sehr geringen plastischen Verformungsanteil. Der Nachteil ist eine im Allgemeinen deutlich größere Querdehnung. Die Behinderung dieser Querdehnung kann in den Rohrstirnflächen zusätzliche … |
|||
|
|
23.11.2005 Bei Vortrieben mit ein- oder mehrsinnig, einfach oder mehrfach gekrümmter Linienführung werden die Druckübertragungsringe durch unterschiedliche Spannungen über den Querschnitt belastet. Da die Belastung und damit die plastischen Verformungen an den Rohrkämpfern (bei horizontale Krümmung) oder an Rohrscheitel und -sohle (vertikaler Krümmung) größer sind (Bild 14.3.2.3), werden die Druckübertragungsringe durch die unterschiedliche Belastung im Laufe … |
|||
|
|
Die Erfahrungen mit der Anwendung der in den vorangegangenen Abschnitten erläuterten Berechnungsansätze haben gezeigt, dass diese mit Unzulänglichkeiten - insbesondere hinsichtlich der Erfassung des Steifigkeitsverhaltens des Systems bestehend aus Rohr und Druckübertragungsring - behaftet sind, die zu teilweise gravierenden Fehleinschätzungen der zulässigen Vortriebskraft führen können. Dies veranlasste die Entwicklung des nachfolgend vorgestellten … |
|||
|
|
(Bild: Querschnittsfunktion in Abhängigkeit von der z-Koordinate für das Berechnungsbeispiel)Um die Spannungsverteilung über den Querschnitt berechnen zu können, ist es zunächst erforderlich, für den vorgegebenen Querschnitt die Geometrie mit einer Funktion in Abhängigkeit von der Durchmesserkoordinate z entsprechend (Bild 14.3.3.1) zu beschreiben, wobei im Falle des Kreisringquerschnittes die z-Achse mit Ursprung am Außenrand des Querschnitts durch … |
|||
|
|
(Bild: Typisches Spannungs-/Stauchungsverhalten eines Druckübertragungsringes aus Weichholz) Das Spannungs-/Stauchungsverhalten in der Praxis eingesetzter Druckübertragungsringe ist, wie bereits erwähnt, ausgeprägt nichtlinear. Das Bild 14.3.3.2 zeigt ein typisches Spannungs-Stauchungsdiagramm für einen Druckübertragungsring aus Fichtenholz mit einer Dicke von sD = 30 mm, das den nachfolgenden Beispielrechnungen zugrunde gelegt wurde. Die Ermittlung … |
|||
|
|
Der Verlauf der Stauchung des Druckübertragungsringes über den Durchmesser und damit die Funktion εD(z) ist grundsätzlich in zwei Abschnitte zu unterteilen:
|
|||
|
|
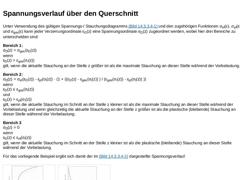
Unter Verwendung des gültigen Spannungs-/ Stauchungsdiagramms (Bild 14.3.3.4) und den zugehörigen Funktionen σel(ε), σpl(ε) und σges(ε) kann jeder Verzerrungsordinate εD(z) eine Spannungsordinate σD(z) zugeordnet werden, wobei hier drei Bereiche zu unterscheiden sind: Bereich 1: |
|||
|
|
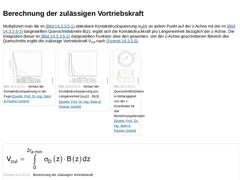
Multipliziert man die im Bild 14.3.3.5 ablesbare Kontaktdruckspannung σD(z) an jedem Punkt auf der z-Achse mit der im Bild 14.3.3.5 dargestellten Querschnittsbreite B(z), ergibt sich die Kontaktdruckkraft pro Längeneinheit bezüglich der z-Achse. Die Integration dieser im Bild 14.3.3.5 dargestellten Funktion über den gesamten, von der z-Achse geschnittenen Bereich des Querschnitts ergibt die zulässige Vortriebskraft Vzul nach Formel 14.3.3.5.
|
|||
|
|
Im Gegensatz zu dem vorgestellten allgemeinen Berechnungsverfahren nach S&P (CoJack) kann in der Berechnungsmethode des ATV-A 161 [ATVA161] und der zugrundeliegenden Theorie von Scherle [Scher90] nur ein konstanter, von der Vorbelastung unabhängiger Elastizitätsmodul für den Druckübertragungsring angesetzt werden. Seine zahlenmäßige Bestimmung ist selbst unter Kenntnis der Spannungs-/Stauchungskurven sehr schwierig und erfolgt daher meist in Form … |
|||
|
|
Besteht eine Vortriebsstrecke aus mehreren hintereinander angeordneten Vortriebsabschnitten mit unterschiedlichen Trassierungselementen (Gerade, Linkskurve, Rechtskurve), kann bezüglich einer Rohrfuge für jeden zu durchfahrenden Abschnitt eine separate Berechnung durchgeführt werden, wobei die bleibenden Auswirkungen aus allen zuvor passierten Teilstrecken berücksichtigt werden können. So ist es beispielsweise problemlos möglich, die Rohrbeanspruchung … |
|||
|
|
Nicht nur die Dicke sondern auch der Werkstoff des Druckübertragungsringes übt einen maßgebenden Einfluss auf die zulässige Vortriebskraft und damit auf die Wirtschaftlichkeit der Vortriebsmaßnahme aus. Unter Zugrundelegung typischer Spannungs-Stauchungsdiagramme von etwa 30 mm dicken Druckübertragungsringen
ermöglicht das allgemeine Berechnungsverfahren … |
|||
|
|
Längskraftschlüssige Rohrverbindungen werden z.B. bei Stahl- oder Kunststoffrohren durch Verschweißen oder Verkleben der Rohrenden hergestellt. Hierbei handelt es sich um starre Rohrverbindungen (Abschnitt 13.2), die beim hier betrachteten Vortrieb durch Einpressen oder Einschieben in der Regel eine planmäßig gerade Linienführung bedingen. Trotzdem sind nach ATV-A 161 [ATVA161] auch in diesem Fall aufgrund unvermeidbarer Steuerkorrekturen Ausmittigkeiten … |
|||
|
|
Bei druckkraftschlüssigen sowie bei längskraftschlüssigen Rohrverbindungen von Stahlrohren ist die Vergleichsspannung nach ATV-A 161 [ATVA161] wie in Formel 14.3.5 nachzuweisen: (Formel: Nachweis der Vergleichsspannung bei druckkraftschlüssigen sowie längskraftschlüssigen Rohrverbindungen von Stahlrohren nach ATV-A 161 [ATVA161]) |
|||
|
|
Vortriebsrohre mit vom Kreisring abweichendem Querschnitt werden im ATV-A 161 [ATVA161] nicht erfasst. Rohre mit kreisförmiger Außenkontur und von der Kreisform abweichender Innenkontur (z.B. Eiquerschnitt, Drachenquerschnitt (Abschnitt 13.3.1.2)) können rechnerisch auf einen Kreisringquerschnitt zurückgeführt werden, wobei der Innenradius durch die kleinste Wanddicke bestimmt wird. Da in Zukunft verstärkt mit dem Einsatz von Vortriebsrohren mit … |
|||
|
|
23.11.2005 Die Berechnung von Vortriebsrohren mit Hohlkastenquerschnitt erfolgt weitestgehend analog zu solchen mit Kreisringquerschnitt mit Ausnahme der:
|
|||
|
|
Aus der Darstellung des Einflusses der Vertikal- und Horizontalbelastung auf den Verlauf der Biegemomente beim Rechteckquerschnitt im Bild 14.4.1.1, Bild 14.4.1.1 und Bild 14.4.1.1 kann abgeleitet werden, dass sich horizontale Lasten in diesem Fall nicht unbedingt wie bei Kreisringquerschnitten (Abschnitt 14.1.2) beanspruchungsmindernd auswirken.
|
|||
|
|
Die im Abschnitt 14.1.5.1 angegebenen Diagramme (Bild 14.1.5.1) (Bild 14.1.5.1) (Bild 14.1.5.1) (Bild 14.1.5.1) zur Bestimmung der Bodenspannung infolge Verkehrslast dürfen nicht auf Hohlkastenquerschnitte übertragen werden, weil die bei Kreisringquerschnitten über den Umfang ungleichförmig verteilte Belastung auf momentengleiche Vollbelastungen umgerechnet wurde. In [Achm92a] wird empfohlen, die Verkehrslasten entsprechend Bild 14.4.1.2 anzusetzen. … |
|||
|
|
Da nur bei rotationssymmetrischen Querschnitten die Bestimmungsgleichung für die Lage der neutralen Faser von der Richtung der Abwinkelung unabhängig ist, ist beim Hohlkastenquerschnitt nicht nur die Koordinate, sondern auch ihre Orientierung zu bestimmen. Um das maßgebende Spannungsverhältnis analog Bild 14.4.1.3 zu berechnen, ist es erforderlich, für das jeweils zu verwendende Hohlkastenprofil ein eigenes, diesbezügliches Diagramm zu erstellen. … |
|||
|
|
Die in den Abschnitt 14.1, Abschnitt 14.2, Abschnitt 14.3 und Abschnitt 14.4 dargestellten Berechnungen … |
|||
|
|
Bei Herstellung von Bohrungen nach dem Bodenverdrängungsverfahren wird das Boden- bzw. Gesteinsmaterial nicht nach über Tage ausgetragen, sondern unter Verdichtung des angrenzenden Baugrundes in die unmittelbare Umgebung des Bohrloches verdrängt. In dieses so hergestellte Bohrloch wird in der Regel sofort mit dem Verdrängungskörper oder anschließend mit einem Aufweitungsteil die Leitung mit geringerem Außendurchmesser (mit Überschnitt) oder gleichem … |
|||
|
|
||||
|
|
Durch die Verdrängung und Verdichtung des Bodens kann im Unterschied zu den Bodenentnahmeverfahren nicht von einer Abminderung der Erdlast infolge von Lastumlagerungen ausgegangen werden. Stattdessen wird ein erhöhter Erddruck aktiviert mit der Folge einer größeren Rohrbelastung im Vergleich zum primären Spannungszustand Der erhöhte Erddruck kann berechnet werden:
|
|||
|
|
Die bodenmechanischen Vorgänge bei der Bodenverdrängung sind mit denen bei der Durchführung eines Pressiometer-Versuches [Bague87] [Vesic72] vergleichbar. Ausgangssituation der Berechnungen stellt ein inhomogener Primärspannungszustand dar. Betrachtet man eine radialsymmetrische Aufweitung innerhalb eines Halbraumes mit dem genannten Primärspannungszustand, werden im Boden durch die eingeprägten Verformungen zusätzliche Spannungen (sekundärer Spannungs- … |
|||
|
|
Erfolgt der Vortrieb der Rohrleitung durch Einpressen oder Einschieben, wird die Vortriebskraft entsprechend Abschnitt 14.2 berechnet. Beim Vortrieb durch Einziehen der Rohrleitung wird die erforderliche Einziehkraft (T) analog Abschnitt 16.1.6.3 unter zusätzlicher Berücksichtigung der Reibungskräfte (R) infolge der äußeren Erddruckbelastung wie folgt berechnet: T = (Ws + π · da · p) · L · μ mit: |
12739 Suchergebnisse:
